Overcoming Catastrophic Forgetting in Incremental Few-Shot Learning by Finding Flat Minina

Abstract

Incremental few-shot lelarning requires a model to continually recognize new categories with only a few examples provided. To avoid catastrophic forgetting arised from the data scarcity and imbalance in learning, training of the base classes instead of later few should be done in earlier stage. Therefore, search for the flat local minima of the base training objective function first, then fine-tune the model parameters within the flat region on new tasks.

1. Introduction

• Importance of incremental few-shot learining

  Alike from the assumtions of incremental learning, in real situation, suffiecient data is not provided for new classes, which tends to be rare, making it more difficult.

• Challenges

  Catastrophic forgetting, which is a major challenge for incremental learning, happens due to inaccessibility to previous data. The model tends to overfit to new classes, while forgetting old categories, resulting in drastic performance on previous tasks.

• Current research

  Currently, to overcome the forgetting problem, model parameters have strong constraints to prevent the chanve, or small examplars from old classes are gathered and constraints are added on the exemplars. From empirical study, however, an intransigent model trained on only base classes outperforms methods like joint-training method.

• Solution

  For the base training objective function, find a flat around around the minima, where the base classes are supposed to be well separated and loss is small. It can be found by adding noise to model parameters, and jointly optimizing multiple loss functions. Then, fine-tune the model parameters within the flat region, by clamping the parameters after updating them on few-shot tasks.

  This paper includes:

  An empirical study on existing incremental few-shot learning methods and discover that a simple baseline model trained on base classes outperforms the state-of-art, demonstraining the severity of catastrophic forgetting.

  A novel approach of addrressing the catastrophic forgetting problem in the primitive stage, though finding the flat minima region during training on base classes and fine-tuning.

  Comprehensive experimental results on various dataset, and result of performance close to the approximate upper bound.

2. Related Work

• Few-shot learning

  It aims for generalization of learning new categories with a few labeled samples. Currently, many includes optimization-based and metric-based methods. Optimization-based methods achieves fast adapatation to new tasks with small samples by learning a sepecific optimization algorithm, and metric-based approaches exploit different distance metrics like cosine similarity or DeepEMD in the learned metric/embedding space to measure the similarity between samples.

• Incremental learning

  It focuses on continually learning to recognize new classes in newcoming data without forgetting old classes. Previously, many includes multi-class incremental learning and multi-task incremental learning. To overcome catastrophic forgetting, some tried to impose strong constraints on model parameters on the exemplars of old vlasses by restricting the output logits or penalizing changes of embedding angles. However, since training data for new classes are scarce, it would not be a promising way.

• Incremental few-shot learning

  It aims to learn incrementally with few samples. TOPCI uses a neural gas netwirk and preserve the topology of the feature manifold formed by different classes. FSLL selects few model parameters for incremental learning and ensures the parameters to close to the optimal ones. IDLVQC imposes constraints on the saved exemplars of each class by restricting the embedding drift. Zhang et al. proposes the way to fix the embedding netwok for incremental learning.

• Robust optimization

  Flat local minima leads to better generalization capabilities than sharp minima, since it is more robust with the shift of the test loss due to random perturbations.

3. Severity of Catastrophic Forgetting in Incremental Few-Shot Learning

3.1. Problem Statement

Incremental few-shot learning (IFL) model is trained with a sequence of training sessions ${\mathcal{D}^1,\dots,\mathcal{D}^t}$ with $\mathcal{D}^t={z_i=(x_i^t,y_i^t)}$ of example $x_i^t$ of class $y_i^t\in\mathcal{C}^t$. The base session $\mathcal{D}^1$ contains a large number of classes with sufficient training data for each class, and following sessions only have a small number of classes with few training samples per class. The later ones often presented as an N-way K-shot task with small N and K. In each training sessioin t of IFL is finished, the model is evaluated on test samples from all encountered classes $\mathcal{C}=\bigcup_{i=1}^t\mathcal{C}^i$ with assumption of no overlap between classes of different sessions, i.e., $\forall\,i,j\textrm{ with }i\neq\,j, \mathcal{C}^i\cap\mathcal{C}^j=\emptyset$.

Catastrophic forgetting does not disappear in the IFL, since due to the data scarcity, it needs to adapt fast, while forgetting base classes.

3.2. A Simple Baseline Model for IFL

An intransigent model that does not adapt to new tasks is used as a baseline. It only trained in the base session.

In the inference time, the inference is conducted by as simple nearest class mean (NCM) classification algorith. The classifier is given as:

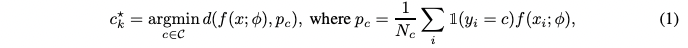
And the baseline model outperformed state-of-the-art IFL and IL methods.

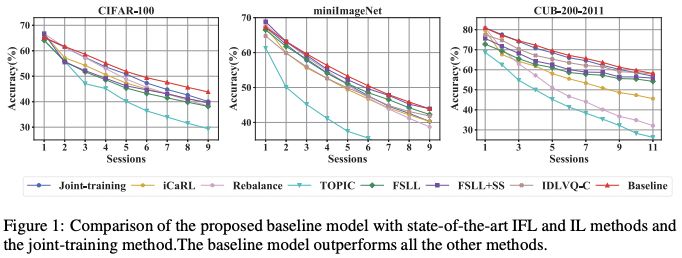
The above suggests:

• For IFL, preserving the old base classes may be more critical than adapting to the new, since the data is scarce, the performance gain on new classes in limited and cannot make up for the loss on base cases.
• Enforcing strong constraints on model parameters or exemplars during fine-tuning on new class did not prevent catastrophic forgetting in IFL.

4. Overcoming Catastrophic Forgetting in IFL by Finding Flat Minima

To overcome catastrophic forgetting, find b-flat local minima $\theta^*$ of the base training objective function and then fine-tune the model within the flat region in later few-shot learning sessions to learn new classes, in short:

\[\theta'=\argmin_\theta\sum_{z\in\mathcal{D}^t}\mathcal{L}(z;\theta)\textrm{ , s.t. }\theta^*-b\preceq\theta\preceq\theta^*+b\]

4.1. Searching for Flat Local Minima in the Base Training Stage

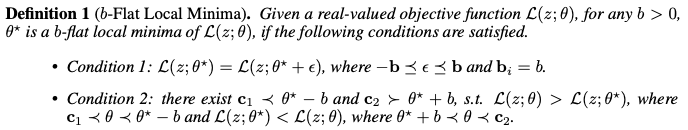
Since the minima is hard to find, by adding noise to the model parameters would aprroximately find the flat minima. Assume the model is parameterized by $\theta={\phi,\psi}$ of the parameters of the embedding network and parameters of the classifier. From the loss function $\mathcal{L}:\mathbb{R}^{d_z}\rightarrow\mathbb{R}$, the target minimized is the expected loss $R:\R^d\rightarrow\R$.

\[R(\theta)=\int_{\R^{d_\epsilon}}\int_{\R^{d_z}}\mathcal{L}(z;\phi+\epsilon,\psi)dP(z)dP(\epsilon)=\mathbb{E}[\mathcal{L}(z;\phi+\epsilon,\psi)]\]

and its estimated empirical loss is given as:

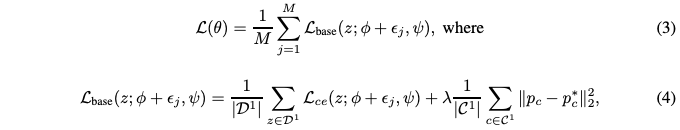
$\mathcal{L}_{ce}(z;\phi+\epsilon_j,\psi)$ is the cross-entrophy loss of a training sample z and $p_c, p_c^*$ are from the class prototypes before and injecting noise respectively.

4.2. Incremental Few-shot Learning within the Flat Region

For the fine-tuning, the loss function is defined as:

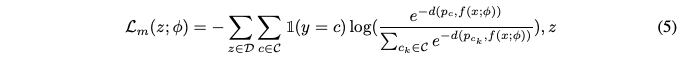
$\mathcal{C}=\bigcup_{i=1}^{t}\mathcal{C}i$ refers to the all encountered classes, and $\mathcal{D}=\mathcal{D}^t\bigcup\mathcal{P}$ is the union of the current data and the exmplar set $\mathcal{P}={P_2, \dots, P{t-1}}$ of all saved esemplars.

After updating the embedding network parameters, the parameters should be clamped to ensure in the flat region of $\phi^-b\preceq\phi\preceq\phi^$ with the optimal parameter vector $\phi^*$ learned in the base session. When fine-tuning is done, evaluating the model by using the nearest class mean classifier.

4.3. Convergence Analysis

For each batch k, let the batch data as $z_k$, and the sampled noises as ${\epsilon_j}_{j=1}^M$, and $\alpha_k$ be the step size. Then the model parameters are updated as:

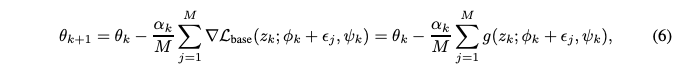
with gradient $g(z_k;\phi_k+\epsilon_j,\psi_k)=\nabla\mathcal{L}_{base}(z_k;\phi_k+\epsilon_j,\psi_k)$.

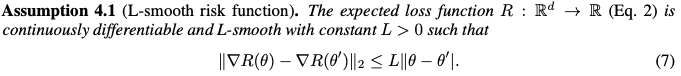
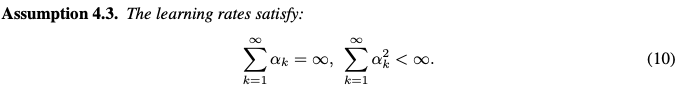
With above assumptions, following theorem can be derived:

• Proof of Throrem 4.1.

  

  

  

  

  

5. Experiments

5.1. Experimental Setup

For the datasets, CIFAR-100 and mini ImageNet was used, and selected 60 classes for the base and reamining 40 as the new classes. Then constructed 5-way 5-shot tasks.

For the baseline, the baseline proposed in Sec. 3 and joint training method is used.

In the base training stage, last 4 or 8 convolution layers were selected to inject noise, since these payers output higher-level feature representations.

5.2. Comparison with the State-of-the-Art

F2M method outperformed the previous SOTA.

5.3. Ablation Study and Analysis

To see the F2M yields more flat minima than the Baseline, the flatness of the local minima was measured for 1000 times with injecting sampled noises. Calculating the indicator $I=\frac{1}{1000}\sum_{i=1}^{1000}(\mathcal{L}i-\mathcal{L}^*)^2$ and variance $\sigma^2=\frac{1}{1000}\sum{i=1}^{1000}(\mathcal{L}_i-\bar{\mathcal{L}})^2$ could be one of the method.

With the ablation of each desings, finding b-falt local minima, prototype fixing term, parameter clamping, prototype normalization, all of those seemed to be effective.

6. Conclusion

Although it was helpful to IFL tasks, but it can not be suitable to medium or high shot tasks, since the flat region is relatively small and it restricts the model capacity. Other methods like elastic weight consolidation can be used to constraint the model parameters.